【印刷可能】 分枝限定法 ナップサック 277851

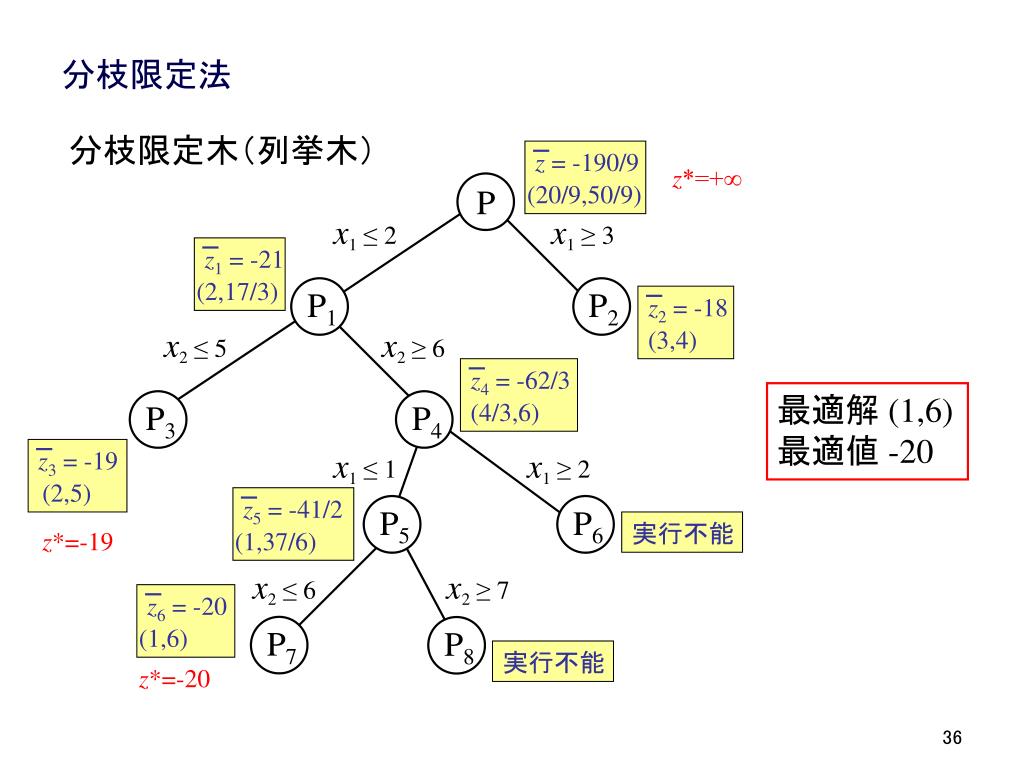
;n) ナップサック問題の解は変数の整数条件を外した 線形最適化問題の解とは一般には一致しない 欲張り法も最適解が得られる保証はない分枝操作： ∈0,1のいくつかを固定 緩和：連続化 ∈0,1により解の上界を与える –連続緩和した問題は簡単に解ける（重いほうから詰める） 分枝限定法の別の例： ナップサック問題次のナップサック問題を分枝限定法によって解く。分枝方法は、連続緩和問題の最適解 において01 条件を満たさない変数を0 と1 に固定することによって行う（右子問題では 分枝変数=1、左子問題では分枝変数=0 とし、左子問題の問題番号が右子問題よりも

第2回 ナップサック問題を色々な方法で解いてみた ブレインパッドの数理最適化ブログ Platinum Data Blog By Brainpad

分枝限定法 ナップサック

分枝限定法 ナップサック-次のナップサック問題を分枝限定法により解け。 （問題 KP0 ）max 15x 118x 26x 32x 4 subject to 4 1 x5x 22x 3x 4 ≦ 6 1, xx 2, x 3, x 4 ∈{0,1} ただし、子問題選択は以下の規則に従うこと。 (1) 奥行優先則 (2) 幅優先則 演習課題 62 次のナップサック問題を動的切除平面法，分枝限定法 分枝カット法 解きやすさ （理論的） （実際的） easy (P) hard (NP) 大規模問題も解ける 解ける問題規模が拡大中 1947年 単体法（Dantzig） 1957～60年 分枝限定法（MarkowitzManne, Eastman, LandDoig） 切除平面法（Gomory） 「はじめよう」 の理由

1995 号 最適解探索方式および最適解探索方法 Astamuse

 前回 最適化：非線形計画問題のメモ 雑なメモ 最適化：非線形計画問題のメモ 雑なメモ など。ほんとにメモ程度なので、厳密だったりしないし記号の定義などもかなり略、だけど講義の内容は大体ふれてるはず。参考文献、引用文献元は記事末尾参照。 役に立ちそうな文献 中央大学理工Private static boolean result; (動的計画法では主に計算時間を、ビット演算ではメモリの使用について考えられると思う) Pomato_b 1426 C言語でサイゼリヤナップサック問題再帰

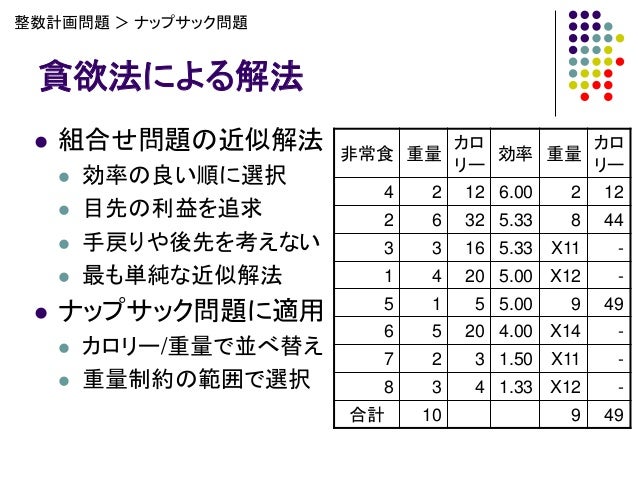
ナップサック問題を分枝限定法で解く アイテム ガム あめ りんご パフ とろり チョコ 山盛り 煎餅 いも チップラムネ しっとり クッキー 値段aj (十円) 5 1 13 15 8 7 21 価値cj 2 1 8 7 4 6 3 8 効率cj/aj 040 100 062 035 027 075 043 038 貪欲アルゴリズムを使って求めた解Part 4 組合せ最適化，41 節 分枝限定法 pp 補助資料：組合せ最適化短編集（朝倉書店）ナップサック問題（クマさん人形泥棒のお話） Part 4では組合せ最適化の種々の技法を解説 ここでは，01ナップサック問題を例として分枝限定法についてを解説．Private static void backtrack(int i, double profit, double weight){

 単体法（ 当連載第4回でご紹介しました ）と分枝限定法が発案された後に、最適化問題を解くための汎用ソフトウェアである数理最適ソルバが登場します。 数理最適ソルバは数理計画法と共に進歩し、様々なソフトウェアが競い合うように発展してきまし図1 01 ナップサック問題に対する分枝木 31 分枝限定法 分枝限定法は，一部の変数を固定しつつそれぞ れの場合を調べ上げていくという考え方に基づい ている．この過程は，図1 のような図（分枝木と 呼ぶ）を用いて表現できる．一番上の点1は元の さて、いよいよ次からナップサック問題を考えてみましょう。 2 ナップサック問題 ナップサック問題の登場までが長くなってしまいましたが、本来 dp 以外で簡単に解ける問題を敢えて dp で解いたのは、ナップサック問題に対する dp はこれよりも一段難易度が上がるからです。

最も欲しかった 分枝限定法 ナップサック C 分枝限定法 ナップサック C Mbaheblogjpq0gu

2

組合せ最適化関連図 問題例（1） ナップサック問題 計算量の壁 アルゴリズムの重要性 問題例（2） 巡回セールスマン問題 tsp 研究の最前線 分枝限定法 局所探索法 最適解の概念図 数理計画法との関連 計算の複雑さの理論 最近の研究紹介 卒業研究 修士論文 解法 分枝限定法（Branch and Bound） まず始めに01ナップサック問題を整数計画問題として定式化します． 整数計画問題 (P) maximize subject to 変数 は値が のとき 番目のアイテムを選択し， のとき選択をしないことに対応しています． 分枝限定法は変数の値を順番に0か1かに固定していき分枝木を) Fë q4 ì e8 Fÿ7´FçFÔ " q40 G" ÓG G FûFÿ ² 4 òH FçG G FôG FçH FÜ ²0 3Æ ºFÿH H Z XH )z g0£#ì e8 FúG G ±0d 0£'ì µFøG0GyGBGxGHGnFþ$Î

難しいナップサック問題はどこにある

動的計画法

分枝限定法 ナップサック問題 最大化z = ∑n i=1 cixi 制約条件 ∑n i=1 aixi b xi 2f0;1g (i = 1;2;2 並列分枝限定法 21 分枝限定法 branchandboundmethod分枝限定法（ ）の基 本的な考え方は，図1に示したように，直接解きがた い問題に表れる整数変数を固定し，より解きやすい部 分問題（partialproblems）に分解する．そしてこの ナップサック問題 とは、ナップサックに容量を超えずに荷物を詰めるときにその荷物の合計価値が最大となる組み合わせを求める 最適化問題 です。 について、貪欲法で解きます。 貪欲法は「重さ当たりの値段が高いものを詰めれば価値が大きくなる」と

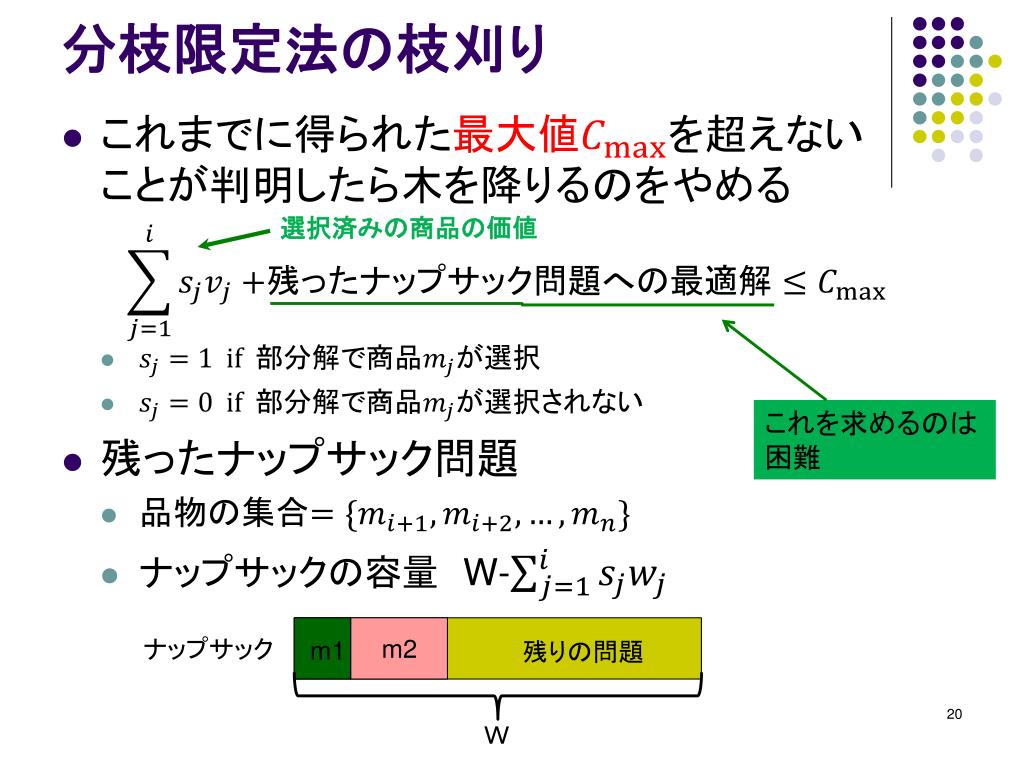
Ppt 情報システム基盤学 基礎 1 アルゴリズムとデータ構造 Powerpoint Presentation Id

2

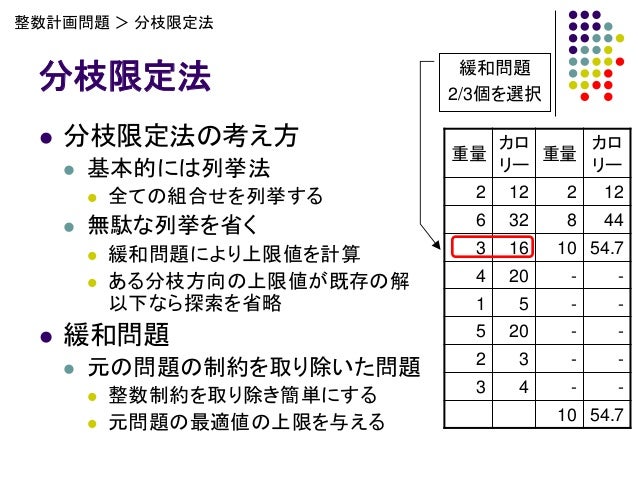
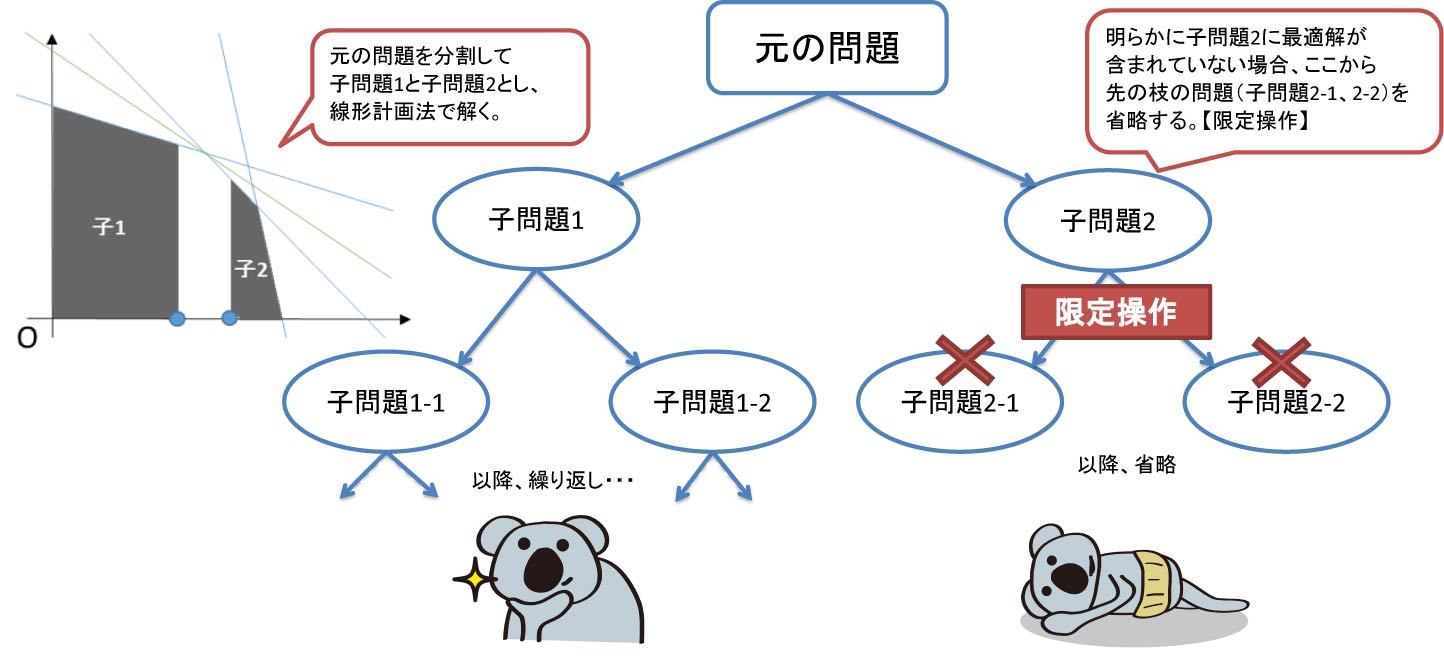
分枝限定法の考え方 整数計画問題（組合せ最適化問題）を，場合分けに よって部分問題に分解（分枝操作） 01ナップサック問題：各変数について0 の場合と1 の場合 に分ける 巡回セールスマン問題：次に訪問する都市によって場合分け分枝限定法 分枝カット法 動的計画法 ．．． 近似解法最適解を求めることを諦めて，ある程度最適値に近い値をもつ実 行可能解をなるべく早く求める 制度保証付き近似解法 メタヒューリスティック（タブーサーチ，遺伝的アルゴリズ ム，アニーリング法分枝限定法の考え方 • 組合せ計画問題を，場合分けによって部分問題に分解 （分枝操作） • 01ナップサック問題：各変数について0 の場合と1 の場合に分 ける • 分枝の進行の様子は探索木により表現可能 • これだけでは，解の全列挙と同じで時間がかかる

ナップサック問題に対する分枝限定法 Youtube

第2回 ナップサック問題を色々な方法で解いてみた ブレインパッドの数理最適化ブログ Platinum Data Blog By Brainpad

I分枝限定法の原理を理解する I分枝限定法を用いて整数計画問題が解けるようになる 岡本吉央(電通大) 最適化手法(5) 13 年5 月17 日 2 / 53 概要 今日考えたい問題(準備& 復習) ：ナップサック問題を解く ナップサック問題 最大化 x 3x1 4x2 x3 2x4 条 件2x1 3x2 x3分枝限定法 巡回セールスマンやナップサック問題のような組み合わせ最適化問題を解くことを考える。解の組み合 わせは有限なので、すべての組み合わせを列挙して評価すれば最適解が得られるが、組み合わせの数は 膨大であり効率が悪い。動的計画法と分枝限定法を組合せた厳密解法が提案されている しかし, 実用的な規模の問題 が解かれているわけではない 実用規模の多次元非線形ナップザック問題を厳密に解くことは現実的に不 可能であり, 有効な近似解法の開発が重要である そこで

2

組合せ最適化問題と厳密解法 最小木 ナップサック問題 ビンパッキング 巡回セールスマン問題 Lpによる上界 下界 分枝限定法 Ppt Download

分枝限定法の実装 基本的な分枝限定法として01 ンプルな理解のために発見的な手法による工夫を効率順でのソーティングにしぼったナップサック問題に対する分枝限定法を実装した 今回はよりシ 31 01 基本的な実装 ナヅブサヅク問題は,数理計画と最適化 ー組み合わせ最適化1ー 精密工学科 淺間一 喬晓蕊，岩滝宗一郎，友井大将（TA） asama@robottutokyoacjp 組み合わせ最適化（欲張り法） 授業（5/29），演習（5/30）分列挙法を系統的に繰り返して行う手法が分枝限定法で ある。） ここでは、先ほどの例に対して部分列挙方の考え方を示す。 (1,1,1,1, ,0,02 3 ) x r = 先ほどの、線形緩和で得られた緩和解は、 によって、緩和解の切り捨によって、上界値90を求 めることができ

動的計画法 ナップサック問題 アルゴリズム講習会

公開鍵暗号3 ナップザック暗号

• 重さあたりの価値で分枝限定法を使う 7 public class KnapsackBB { // 01ナップザック問題を分枝限定法で解く private static double maxsofar;64 ナップザック問題を解く分枝限定法(branch{and{bound method) (a) 上界と下界 ナップザック問題の緩和問題を考える (KP) max z = ∑n j=1 cjx j s t ∑n j=1 aj xj b 0 x j 1,j = 1,2, ,n この問題の最適解は次のようにして簡単に得られる．不等式 P∑−1 j=1 aj b < ∑P j=1 aj分枝操作： ∈0,1のいくつかを固定 緩和：連続化 ∈0,1により解の上界を与える –連続緩和した問題は簡単（𝑞 / が大きい方から詰める） 分枝限定法の別の例： ナップサック問題

ナップサック問題 Opt100

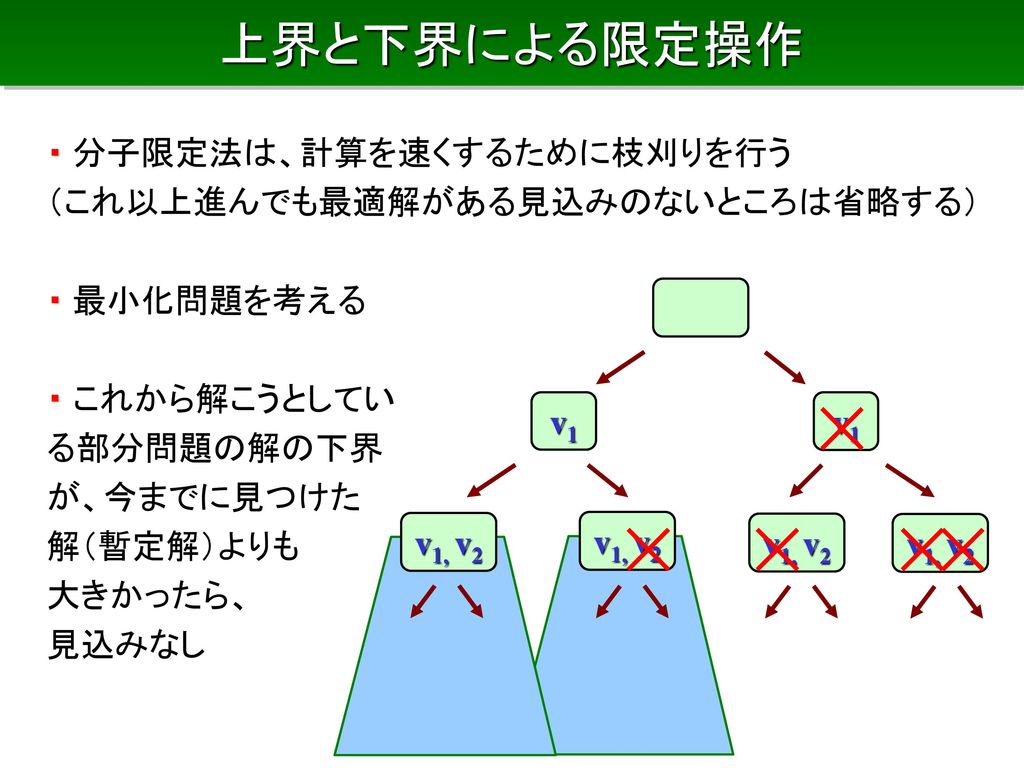
組合せ最適化問題と厳密解法 最小木 ナップサック問題 ビンパッキング 巡回セールスマン問題 Lpによる上界 下界 分枝限定法 Ppt Download

分枝限定法の考え方 •問題を場合分けによって部分問題に分解（分枝操作） •01ナップサック問題： 各変数について0 の場合と1 の場合に分ける •分枝の進行の様子は探索木により表現可能 •これだけでは解の全列挙と同じ，時間がかかる分枝限定法の考え方 • 組合せ計画問題を，場合分けによって部分問題に分解 （分枝操作） • 01ナップサック問題：各変数について0 の場合と1 の場合に分 ける • 巡回セールスマン問題：次に訪問する都市によって場合分け • 分枝の進行の様子は探索木により表現可能– 分枝限定法では，終端条件を満たしたときは追加を行わない • 手続きの非一義性：頂点を一つ取り出すデータ構造依存 – スタック：深さ優先探索、キュー：幅優先探索 (Ref 杉原厚吉 "データ構造とアルゴリズム", 共立出版) スタック(Stack)

Efficient Algorithms For Combinatorial Optimization Problems Speaker Deck

ナップサック問題に対する分枝限定法 Youtube

数理最適化特論／mathematical optimization 21年度 秋学期 月曜 3時限（1330〜1510） 授業形態 第5回までは完全オンライン，第6回からは基本対面 登録コードMSIS7210 第1回（9月27日） 第2回（10月4日） 第3回（10月11日） 第4回（10月18日） 第5回（10月25日）Private static boolean choice;・分枝限定法：組合せ最適化問題の最適解を求める主要な方法 ・欲張り法：準最適解を求めることができる。最適解が 得られる保証はない。 ・吝嗇法：欲張り法の逆の考え方。最適解が得られる保証は

Ppt 情報システム基盤学 基礎 1 アルゴリズムとデータ構造 Powerpoint Presentation Id

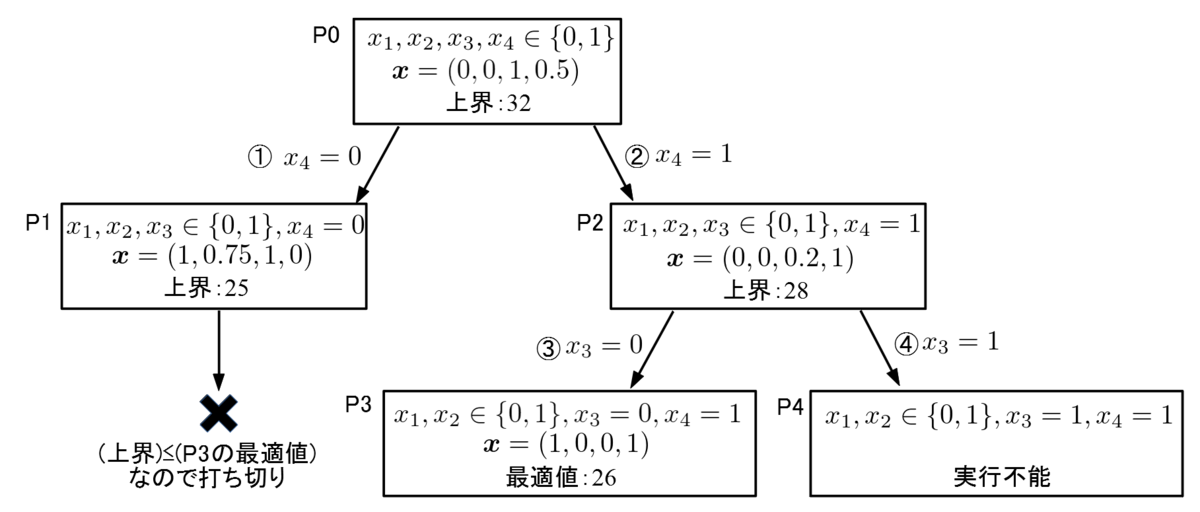
ナップサック問題と分枝限定法 Helve Tech Blog

多目的ナップサック問題を解くために動的計画法や分枝限定法をもとにしたアルゴリズム が開発されてきた1 l かしこれらの多くは, 線形なナップサック問題を扱うものであった また, 多次元非線形ナップサック問題においては, これらの手法は有効ではなく,

最も欲しかった 分枝限定法 ナップサック C 分枝限定法 ナップサック C Mbaheblogjpq0gu

2

2

最も人気のある 分枝限定法 ナップサック 分枝限定法 ナップサック Java Blogjpmbahe3gsl

第2回 ナップサック問題を色々な方法で解いてみた ブレインパッドの数理最適化ブログ Platinum Data Blog By Brainpad

6 Info Shako

Amazon Co Jp 数学的最適化

Branch And Bound Algorithm And Cutting Plane Algorithm For Integer Programs Speaker Deck

2

Operations Research Yonezawa No2

Ppt 最適化ワークショップ 整数計画法の発展と応用 整数計画法チュートリアル モデリングと解法 Powerpoint Presentation Id

Operations Research Yonezawa No2

Branch And Bound Algorithm And Cutting Plane Algorithm For Integer Programs Speaker Deck

ナップサック問題に対する分枝限定法 Youtube

7 3 分枝限定法の並列化の利用

Branch And Bound Algorithm And Cutting Plane Algorithm For Integer Programs Speaker Deck

難しいナップサック問題はどこにある

第2回 ナップサック問題を色々な方法で解いてみた ブレインパッドの数理最適化ブログ Platinum Data Blog By Brainpad

生産スケジューラーflexsche無料体験セミナーin四国 貴社ビジネスのit共創者 中央コンピューター株式会社

組合せ最適化問題と厳密解法 最小木 ナップサック問題 ビンパッキング 巡回セールスマン問題 Lpによる上界 下界 分枝限定法 Ppt Download

B 2 3 分枝限定法

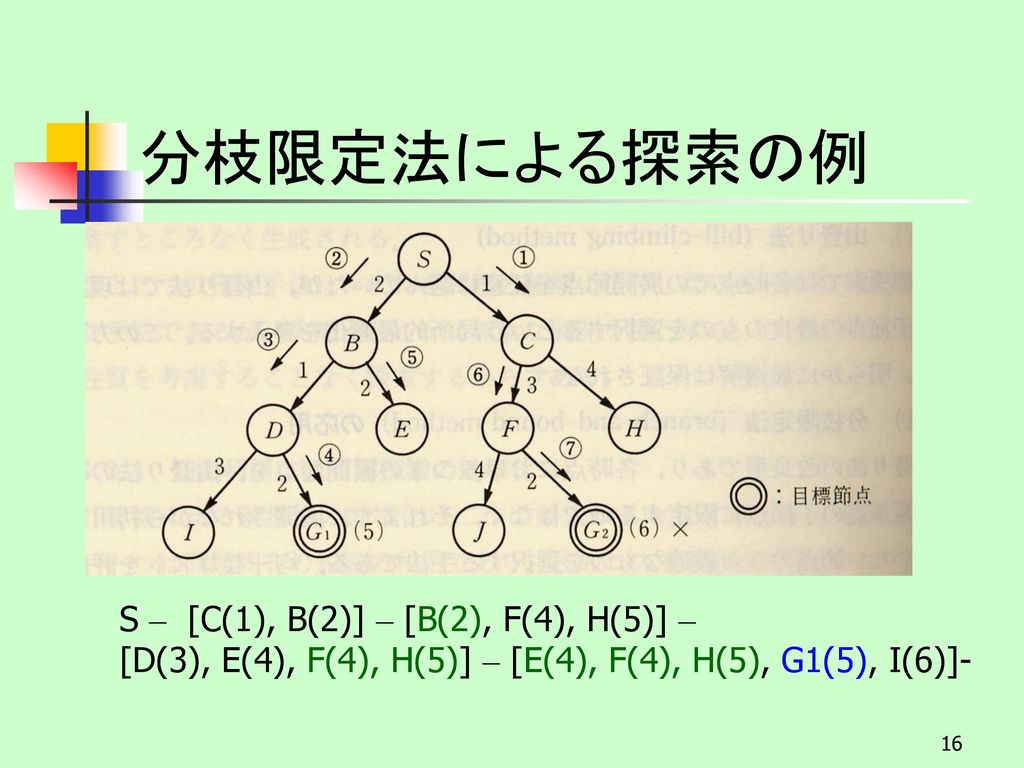
最も欲しかった 分枝限定法 ナップサック C 分枝限定法 ナップサック C Mbaheblogjpq0gu

Operations Research Yonezawa No2

Np完全やnp困難な 問題の最適解を 得るのは困難 近似解法

ナップサック問題に対する分枝限定法 Youtube

Atcoder Abc32 D ナップザック問題を分岐限定法で爆速で解く Qiita

組合せ最適化問題と厳密解法 最小木 ナップサック問題 ビンパッキング 巡回セールスマン問題 Lpによる上界 下界 分枝限定法 Ppt Download

ソフトウェアii 第4回 12 10 ソフトウェアii

難しいナップサック問題はどこにある

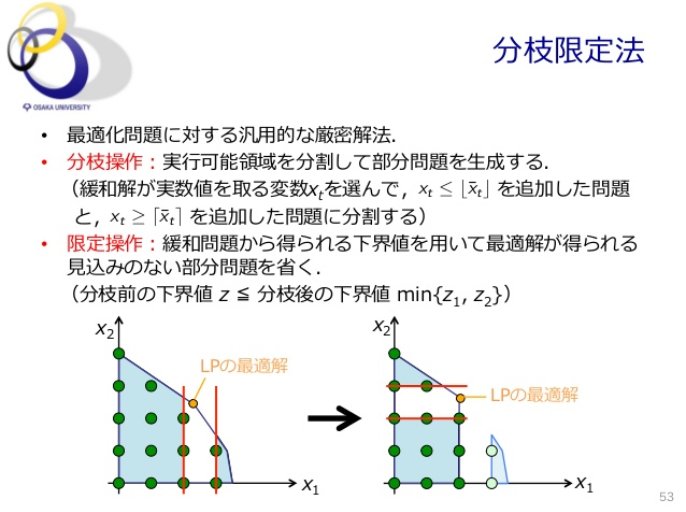
最も人気のある 分枝限定法 ナップサック 分枝限定法 ナップサック Java Blogjpmbahe3gsl

1995 号 最適解探索方式および最適解探索方法 Astamuse

図で見る分枝限定法 Qiita

2

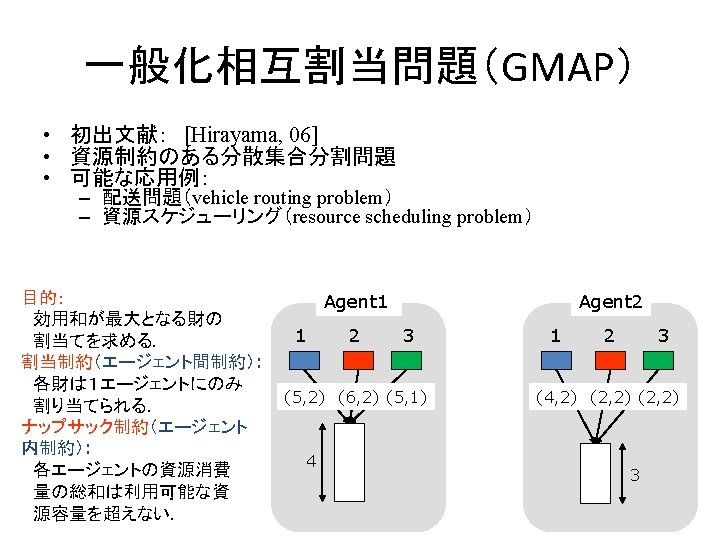
Dcop Adopt Modi 03 Bn Badopt Yeoh 10

2

最も人気のある 分枝限定法 ナップサック 分枝限定法 ナップサック Java Blogjpmbahe3gsl

2

Branch And Bound Algorithm And Cutting Plane Algorithm For Integer Programs Speaker Deck

2

混合整数線形計画法 Mip アルゴリズム 入門

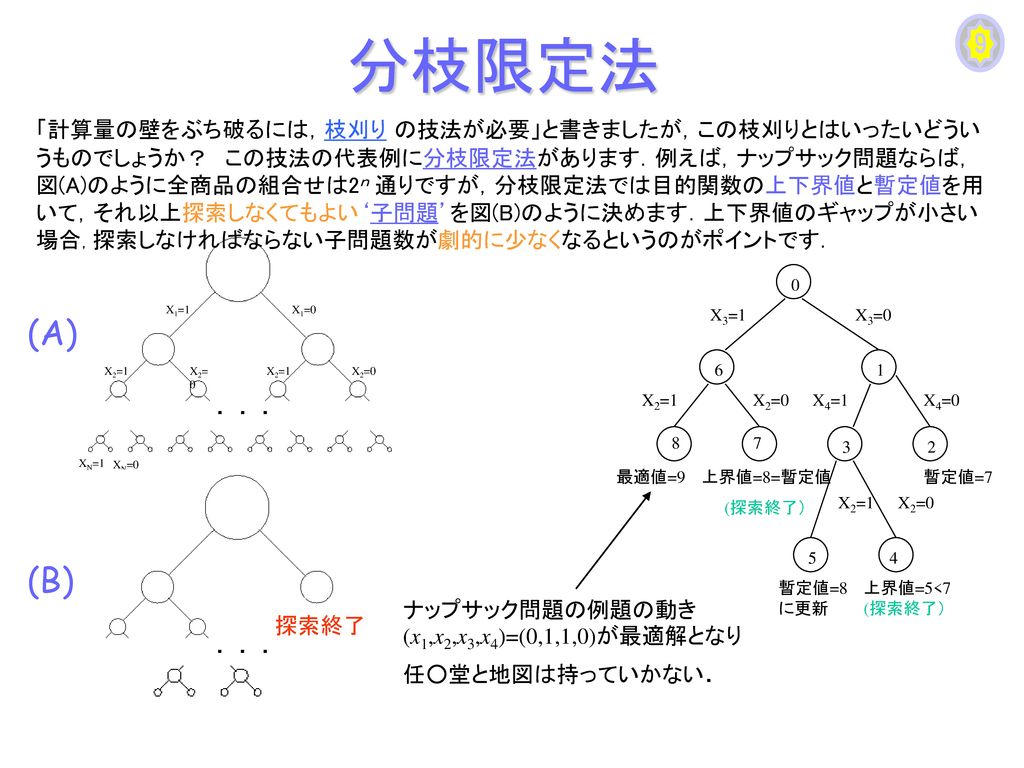
1 ｗｅｌｃｏｍｅ 情報数理研究室 理工学3号館1階北側中央部分 Ppt Download

Efficient Algorithms For Combinatorial Optimization Problems Speaker Deck

ナップサック問題に対する分枝限定法 Youtube

図で見る分枝限定法 Qiita

1995 号 最適解探索方式および最適解探索方法 Astamuse

Branch And Bound Algorithm And Cutting Plane Algorithm For Integer Programs Speaker Deck

難しいナップサック問題はどこにある

ナップサック問題に対する分枝限定法 Youtube

04 号 問題分割方法 最適化方法 問題分割装置 最適化装置 及びコンピュータプログラム Astamuse

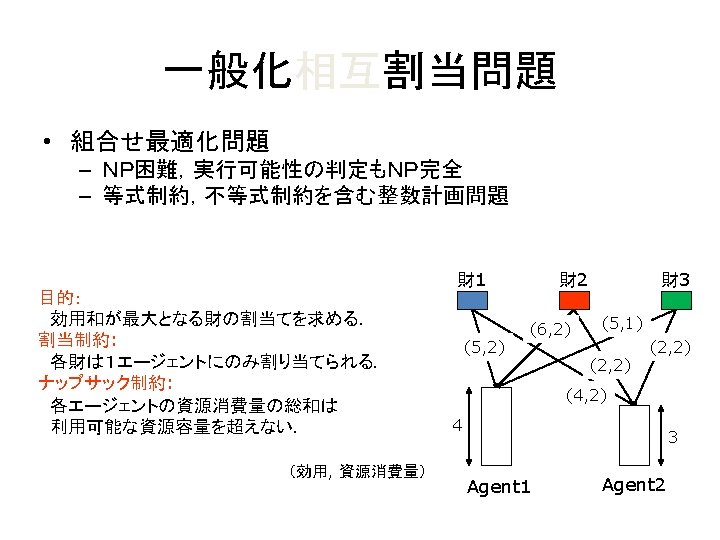
Dcop Adopt Modi 03 Bn Badopt Yeoh 10

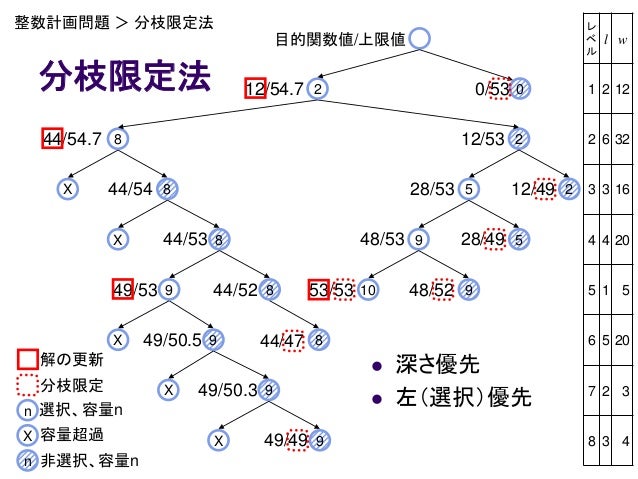
Operations Research Yonezawa No2

難しいナップサック問題はどこにある

問題解決力を鍛える アルゴリズムとデータ構造 書籍情報 株式会社 講談社サイエンティフィク

Ppt 最適化ワークショップ 整数計画法の発展と応用 整数計画法チュートリアル モデリングと解法 Powerpoint Presentation Id

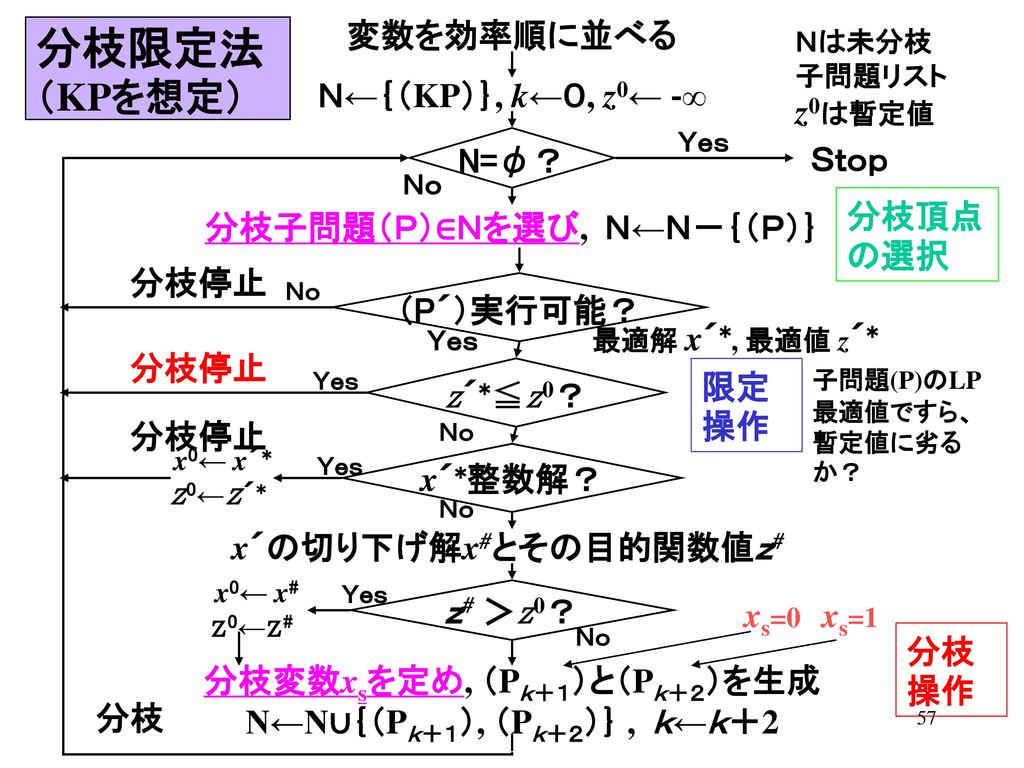
基礎ｏｒ ｏｒ演習 第６回 11 17 09 森戸担当分中間試験 来週 １１ ２４ 火 １３ ００は試験 Ppt Download

2

大きなナップサック 解説 おじい研究所

0 1 ナップザック問題について ２ T Nakaの阿房ブログ

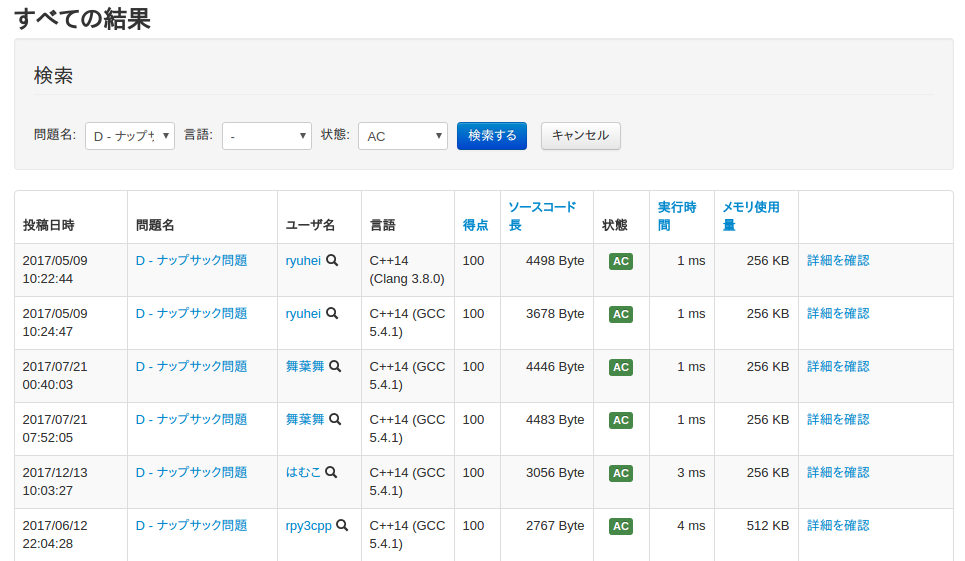
Atcoder Abc32 D ナップザック問題を分岐限定法で爆速で解く Qiita

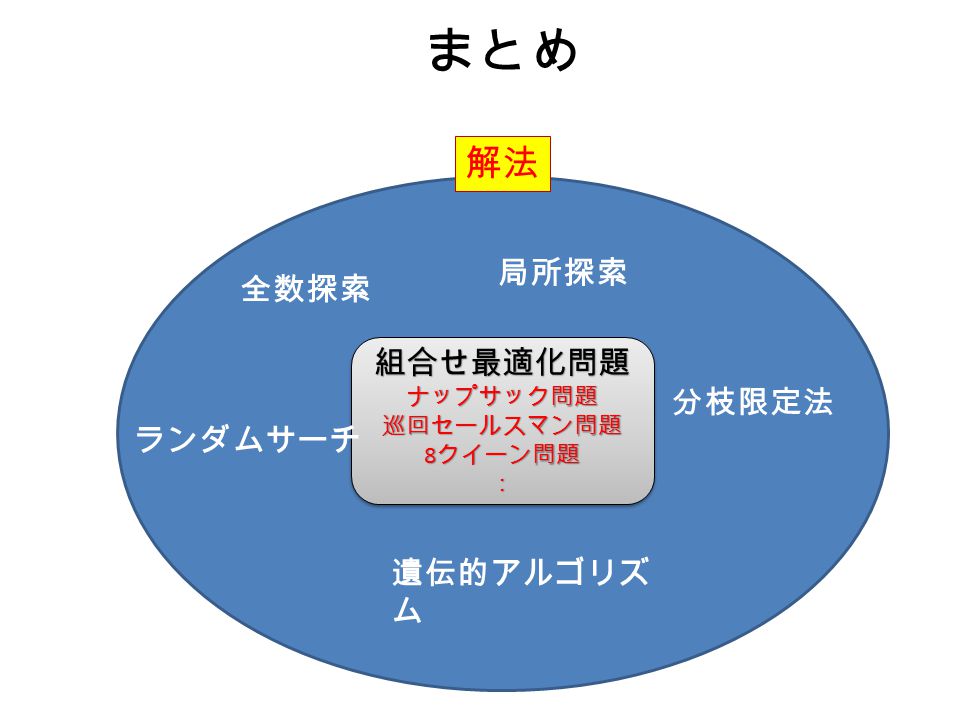
知能情報処理 第1回 この授業の概要 組合せ最適化問題とは Ppt Video Online Download

最も人気のある 分枝限定法 ナップサック 分枝限定法 ナップサック Java Blogjpmbahe3gsl

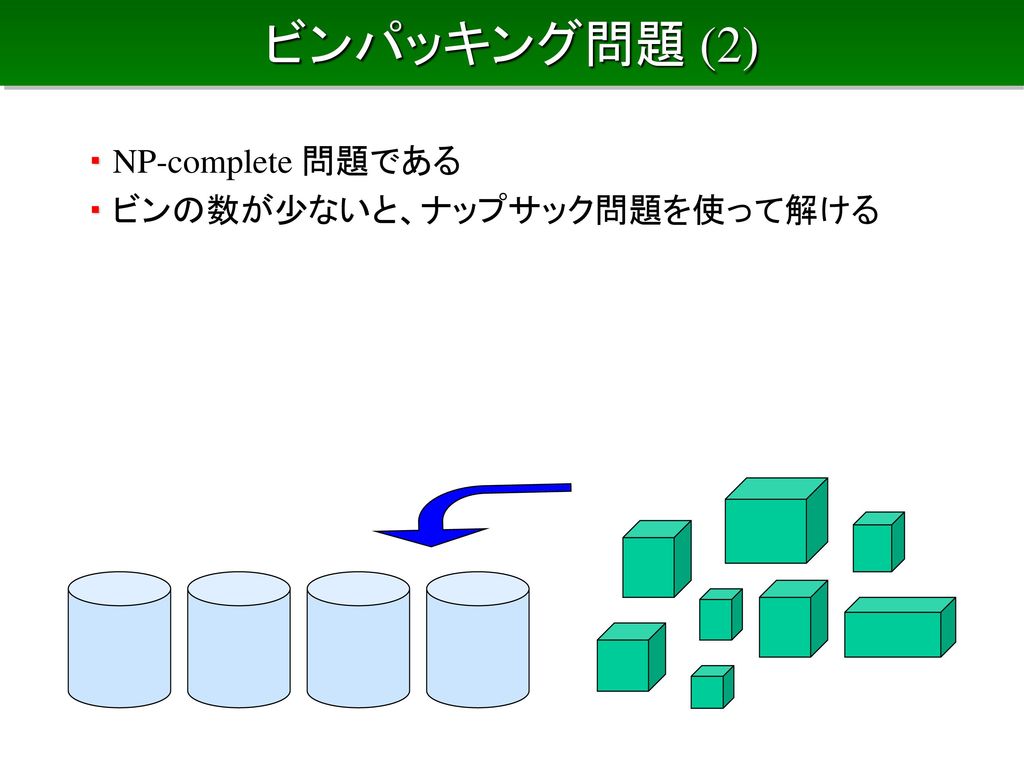
組合せ最適化問題と厳密解法 最小木 ナップサック問題 ビンパッキング 巡回セールスマン問題 Lpによる上界 下界 分枝限定法 Ppt Download

ナップサック問題 クマさん人形をめぐる熱いドラマの結末 Ppt Download

最も欲しかった 分枝限定法 ナップサック C 分枝限定法 ナップサック C Mbaheblogjpq0gu

知能情報処理 第1回 この授業の概要 組合せ最適化問題とは Ppt Video Online Download

第2回 ナップサック問題を色々な方法で解いてみた ブレインパッドの数理最適化ブログ Platinum Data Blog By Brainpad

組合せ最適化問題と厳密解法 最小木 ナップサック問題 ビンパッキング 巡回セールスマン問題 Lpによる上界 下界 分枝限定法 Ppt Download

ナップサック問題に対する分枝限定法 Youtube

ナップサック問題と分枝限定法 Helve Tech Blog

Ppt 情報システム基盤学 基礎 1 アルゴリズムとデータ構造 Powerpoint Presentation Id

知能情報処理 第1回 この授業の概要 組合せ最適化問題とは Ppt Video Online Download

基礎ｏｒ ｏｒ演習 第６回 11 17 09 森戸担当分中間試験 来週 １１ ２４ 火 １３ ００は試験 Ppt Download

ナップサック問題に対する分枝限定法 Youtube

Operations Research Yonezawa No2

2

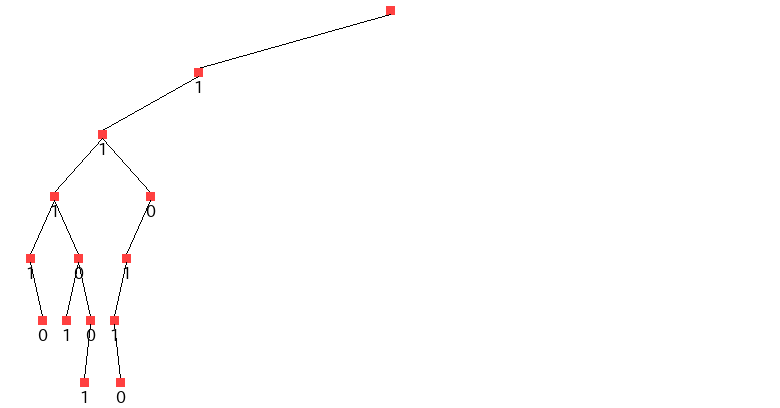
図で見る分枝限定法 Qiita

Ppt 最適化ワークショップ 整数計画法の発展と応用 整数計画法チュートリアル モデリングと解法 Powerpoint Presentation Id

最も人気のある 分枝限定法 ナップサック 分枝限定法 ナップサック Java Blogjpmbahe3gsl

2

Ppt 情報システム基盤学 基礎 1 アルゴリズムとデータ構造 Powerpoint Presentation Id

Operations Research Yonezawa No2

難しいナップサック問題はどこにある